Private key generation from on-line handwritten signatures HaoFeng School of Electrical and Electronic Engineering, Nanyang Technological University, Singapore Chan Choong Wah School of Electrical and Electronic Engineering, Nanyang Technological University, Singapore Introduction The exchanging of computer-based documents such as electronic. As an alternative, researchers advocate the generation of cryptographic key using the biometric traits of both sender and receiver during the sessions of communication, thus avoiding key storing.

Fuzzy commitment scheme for generation of cryptographic keys based on iris biometrics

Fuzzy commitment scheme for generation of cryptographic keys based on iris biometrics

For access to this article, please select a purchase option:

IET members benefit from discounts to all IET publications and free access to E&T Magazine. If you are an IET member, log in to your account and the discounts will automatically be applied.

Thank you

Your recommendation has been sent to your librarian.

This work presents a method based on information-theoretic analysis of iris biometric that aims to extract homogeneous regions of high entropy. Successful extraction of these regions facilitates the development of effective systems for generation of cryptographic keys of lengths up to 400 bits per iris. At the same time, this approach allows for the application of simpler error correction codes with equal false accept rate levels, which reduces the overall complexity of this class of systems.

References

• 1. 1)
     • 1. Soutar, C., Roberge, D., Stoianov, A., et al: ‘Biometric encryption’, in Nichols, R.K. (ed.): ‘ICSA guide to cryptography’ (McGraw-Hill Publishers, New York, 1999).
  2. 2)
     • 2. Davida, G.I., Frankel, Y., Matt., B.J., et al: ‘On the relation of error correction and cryptography to an offline biometric based identification scheme’. In Proceedings of WCC99, Workshop on Coding and Cryptography, 1999.
  3. 3)
     • 3. Hao, F., Anderson, R., Daugman, J.: ‘Combining crypto with biometrics effectively’, IEEE Trans. Comput., 2006, 55, (9), pp. 1081–1088.
  4. 4)
     • 4. Kanade, S., Camara, D., Krichen, E., Petrovska-Delacretaz, D., Dorizzi, B., et al: ‘Three factor scheme for biometric-based cryptographic key regeneration using iris,’ in The 6th Biometrics Symposium 2008 (BSYM2008), September 2008.
  5. 5)
     • 5. Garcia-Baleon, H.A., Alarcon-Aquino, V., Starostenko, O., et al: ‘Bimodal biometric system for cryptographic key generation using wavelet’. IEEE Mexican Int. Conf. on Computer Science, 2009, pp. 186–196.
  6. 6)
     • 6. Hao, F., Chan, C.W.: ‘Private key generation from on-line handwritten signatures’, Inf. Manag. Comput. Sec., 2002, 10, (2), pp. 159–164.
  7. 7)
     • 7. Tuyls, P., Akkermans, A.H.M., Kevenaar, T.A.M., et al: ‘Practical biometric authentication with template protection’. Proc. of the 5th Int. Conf. on Audio- and Video-Based Biometric Person Authentication, AVBPA'05, 2005, pp. 436–446.
  8. 8)
     • 8. van der Veen, M., Kevenaar, T., Schrijen, G.-J., et al: ‘Face biometrics with renewable templates’. Proc. SPIE 6072, Security, Steganography, and Watermarking of Multimedia Contents VIII, 60720J, February 2006.
  9. 9)
     • 9. Monrose, F., Reiter, M.K., Li, Q., et al: ‘Cryptographic key generation from voice’. Proc. of the 2001 IEEE Symp. on Security and Privacy, May 2001.
  10. 10)
      • 10. Clancy, T.C., Kiyavash, N., Lin, D.J.: ‘Secure smart card-based fingerprint authentication’. Proc. ACM SIGMM Workshop Biometrics Methods and Application (WBMA), 2003.
  11. 11)
      • 11. Rathgeb, C., Uhl, A.: ‘Two-factor authentication or how to potentially counterfeit experimental results in biometric systems’. Proc. of the Int. Conf. on Image Analysis and Recognition, 2010, pp. 296–305.
  12. 12)
      • 12. Daugman, J.: ‘The importance of being random’, Stat. Princ. Iris Recognit., Pattern Recognit., 2003, 36, (2), pp. 279–291.
  13. 13)
      • 13. Bringer, J., Chabanne, H., Cohen, G., Kindarji, B., Zemor, G., et al: ‘Theoretical and practical boundaries of binary secure sketches’, IEEE Trans. Inf. Forensics Sec., 20083, (4), pp. 673–683.
  14. 14)
      • 14. Kelkboom, E.J.C., Breebaart, J., Kevenaar, T.A.M., et al: ‘Preventing the decodability attack based cross-matching in a fuzzy commitment scheme’, IEEE Trans. Inf. Forensics Sec., 2011, pp. 107–121.
  15. 15)
      • 15. Rathgeb, C., Uhl, A.: ‘Statistical attack against fuzzy commitment scheme’, IET Biometrics, 2012, pp. 94–104.
  16. 16)
      • 16. Maiorana, E., Campisi, P., Neri, A.: ‘IRIS template protection using a digital modulation paradigm’. 2014 IEEE Int. Conf. on Acoustics, Speech and Signal Processing (ICASSP), Florence, 2014, pp. 3759–3763.
  17. 17)
      • 17. Álvarez Mariño, R., Hernández Álvarez, F., Hernández Encinas, L.: ‘A crypto-biometric scheme based on iris-templates with fuzzy extractors’, Inf. Sci., 2012, 195, pp. 91–102.
  18. 18)
      • 18. Shannon, C.E.: ‘A mathematical theory of communication’, Bell Syst. Techn. J., 1948, 27, pp. 379–423, 623–656.
  19. 19)
      • 19. Shannon, C.E.: ‘Communication theory of secrecy systems’, Bell Syst. Tech. J., 1949, 28, pp. 656–715.
  20. 20)
      • 20. Daugman, J.: ‘How iris recognition works’, IEEE Trans. Circuits Syst. Video Technol., 2004, 14, pp. 21–30.
  21. 21)
      • 21. Gonzalez, R.C., Woods, R.E., Eddins, S.L.: ‘Digital image processing using MATLAB’ (Prentice-Hall, New Jersey, 2003).
  22. 22)
      • 22. Adamovic, S., Milosavljevic, M.: ‘Information analysis of iris biometrics for the needs of cryptology key extraction’, Serb. J. Electr. Eng., 2013, 10, (1), pp. 1–12.
  23. 23)
      • 23. Adamovic, S., Savic, A.G., Milosavljevic, M., et al: ‘Texture analysis of iris biometrics based on adaptive size neighborhood entropy and linear discriminant analysis’. Int. Scientific Conf. – Sinteza, Serbia, April 2014, pp. 658–660.
  24. 24)
      • 24. Masek, L.: ‘Recognition of human iris patterns for biometric identification iris recognition’, http://www.csse.uwa.edu.au/~pk/studentprojects/libor/, accessed 15 October 2012.
  25. 25)
      • 25. Daugman, J.: ‘Uncertainty relation for resolution in space, spatial frequency, and orientation optimized by two-dimensional visual cortical filters’, J. Opt. Soc. Am. A, 1985, 2, (7), pp. 1160–1169.
  26. 26)
      • 26. Juels, A., Wattenberg, M.: ‘A fuzzy commitment scheme’. Proc. of the 6th ACM Conf. on Computer and Communications Security, 1999.
  27. 27)
      • 27. Biometrics Ideal Test, http://biometrics.idealtest.org, accessed 15 October 2013.
  28. 28)
      • 28. Goh, A., Ngo, D.C.L.: ‘Computation of cryptographic keys from face biometrics. communications and multimedia security’. ‘Advanced techniques for network and data protection’ (Springer Berlin Heidelberg, 2003), pp. 1–13.
  29. 29)
      • 29. Zhou, X., Kuijper, A., Veldhuis, R., et al: ‘Quantifying privacy and security of biometric fuzzy commitment’. Biometrics (IJCB), 2011 Int. Joint Conf. on, Washington, DC, 2011, pp. 1–8.

Related content

• Cryptography Tutorial

• Cryptography Useful Resources

Cryptographic Key Generation Using Handwritten Signature Software

• Selected Reading

Digital signatures are the public-key primitives of message authentication. In the physical world, it is common to use handwritten signatures on handwritten or typed messages. They are used to bind signatory to the message.

Similarly, a digital signature is a technique that binds a person/entity to the digital data. This binding can be independently verified by receiver as well as any third party.

Digital signature is a cryptographic value that is calculated from the data and a secret key known only by the signer.

In real world, the receiver of message needs assurance that the message belongs to the sender and he should not be able to repudiate the origination of that message. This requirement is very crucial in business applications, since likelihood of a dispute over exchanged data is very high.

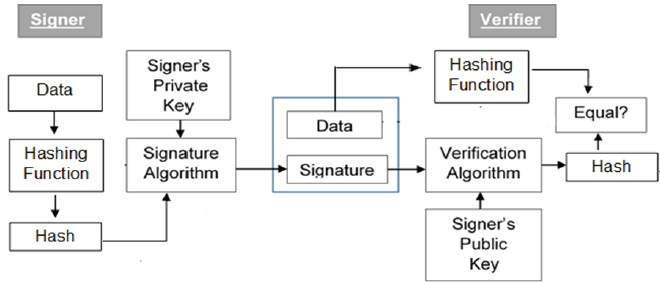
Model of Digital Signature

As mentioned earlier, the digital signature scheme is based on public key cryptography. The model of digital signature scheme is depicted in the following illustration −

The following points explain the entire process in detail −

• Each person adopting this scheme has a public-private key pair.

• Generally, the key pairs used for encryption/decryption and signing/verifying are different. The private key used for signing is referred to as the signature key and the public key as the verification key.

• Signer feeds data to the hash function and generates hash of data.

• Hash value and signature key are then fed to the signature algorithm which produces the digital signature on given hash. Signature is appended to the data and then both are sent to the verifier.

• Verifier feeds the digital signature and the verification key into the verification algorithm. The verification algorithm gives some value as output.

• Verifier also runs same hash function on received data to generate hash value.

• For verification, this hash value and output of verification algorithm are compared. Based on the comparison result, verifier decides whether the digital signature is valid.

• Since digital signature is created by ‘private’ key of signer and no one else can have this key; the signer cannot repudiate signing the data in future.

It should be noticed that instead of signing data directly by signing algorithm, usually a hash of data is created. Since the hash of data is a unique representation of data, it is sufficient to sign the hash in place of data. The most important reason of using hash instead of data directly for signing is efficiency of the scheme.

Let us assume RSA is used as the signing algorithm. As discussed in public key encryption chapter, the encryption/signing process using RSA involves modular exponentiation.

Signing large data through modular exponentiation is computationally expensive and time consuming. The hash of the data is a relatively small digest of the data, hence signing a hash is more efficient than signing the entire data.

Importance of Digital Signature

Out of all cryptographic primitives, the digital signature using public key cryptography is considered as very important and useful tool to achieve information security.

Apart from ability to provide non-repudiation of message, the digital signature also provides message authentication and data integrity. Let us briefly see how this is achieved by the digital signature −

Cryptographic Key Generation Using Handwritten Signature Template

• Message authentication − When the verifier validates the digital signature using public key of a sender, he is assured that signature has been created only by sender who possess the corresponding secret private key and no one else.

• Data Integrity − In case an attacker has access to the data and modifies it, the digital signature verification at receiver end fails. The hash of modified data and the output provided by the verification algorithm will not match. Hence, receiver can safely deny the message assuming that data integrity has been breached.

• Non-repudiation − Since it is assumed that only the signer has the knowledge of the signature key, he can only create unique signature on a given data. Thus the receiver can present data and the digital signature to a third party as evidence if any dispute arises in the future.

By adding public-key encryption to digital signature scheme, we can create a cryptosystem that can provide the four essential elements of security namely − Privacy, Authentication, Integrity, and Non-repudiation.

Encryption with Digital Signature

In many digital communications, it is desirable to exchange an encrypted messages than plaintext to achieve confidentiality. In public key encryption scheme, a public (encryption) key of sender is available in open domain, and hence anyone can spoof his identity and send any encrypted message to the receiver.

Cryptographic Key Generation Using Handwritten Signature Software

This makes it essential for users employing PKC for encryption to seek digital signatures along with encrypted data to be assured of message authentication and non-repudiation. download istumbler for mac free

This can archived by combining digital signatures with encryption scheme. Let us briefly discuss how to achieve this requirement. There are two possibilities, sign-then-encrypt and encrypt-then-sign.

However, the crypto system based on sign-then-encrypt can be exploited by receiver to spoof identity of sender and sent that data to third party. Hence, this method is not preferred. The process of encrypt-then-sign is more reliable and widely adopted. This is depicted in the following illustration −

Cryptographic Key Generation Using Handwritten Signature Free

The receiver after receiving the encrypted data and signature on it, first verifies the signature using sender’s public key. After ensuring the validity of the signature, he then retrieves the data through decryption using his private key.